Two Member Frame - Pin/Pin Top Point Load

Structural Related Articles

$\large{ e = \frac{h}{L} }$
$\large{ \beta = \frac{I_h}{I_v} }$
$\large{ R_A = \frac{ P\;x\; \left[L^2\; \left( 2\; \beta \; e \;+\; 3 \right) \;-\; x^2 \right] }{ 2\;L^2\; \left( \beta \; e \; \;+\; 1 \right) } }$
$\large{ R_D = P - R_A }$
$\large{ H_A = H_D = \frac{ P\;x \; \left(L^2 \;-\; x^2\right) }{ 2\;h\;L^2\; \left( \beta \; e \;+\; 1 \right) } }$
$\large{ M_B = \frac{ P\;x\; \left( L^2 \;-\; x^2 \right) }{ 2\;L^2\; \left( \beta \; e \;+\; 1 \right) } }$
$\large{ M_D = \frac{ x\; \left[ P\; \left( L \;-\; x \right) \;-\; M_C \right] }{ L } }$

Units	English	SI
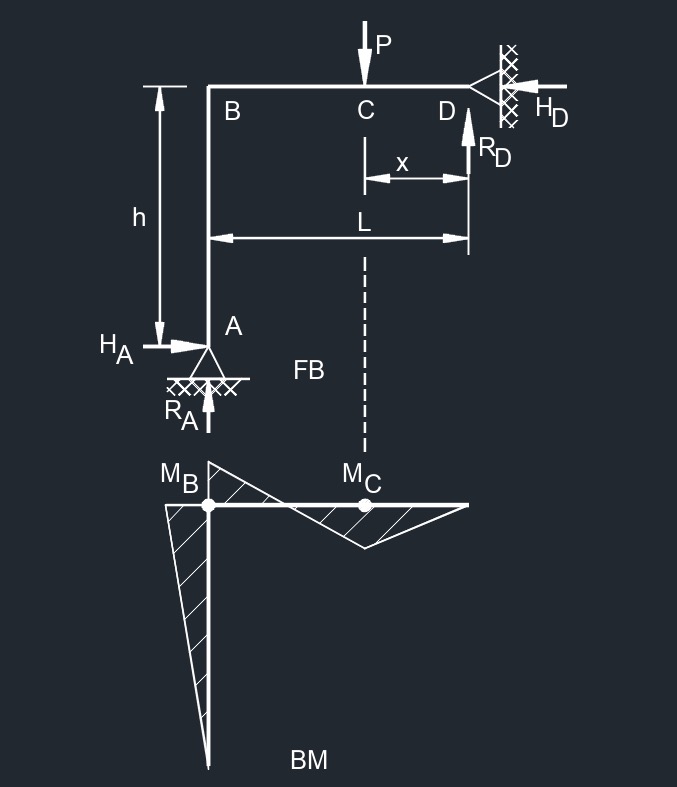
$\large{ FB }$ = free body	-	-
$\large{ BM }$ = bending moment	-	-
$\large{ h }$ = height of frame	$\large{in}$	$\large{mm}$
$\large{ x }$ = horizontal distance from reaction point	$\large{in}$	$\large{mm}$
$\large{ H }$ = horizontal reaction load at bearing point	$\large{lbf}$	$\large{N}$
$\large{ I_h }$ = horizontal member second moment of area (moment of inertia)	$\large{in^4}$	$\large{mm^4}$
$\large{ I_v }$ = vertical member second moment of area (moment of inertia)	$\large{in^4}$	$\large{mm^4}$
$\large{ M }$ = maximum bending moment	$\large{lbf-ft}$	$\large{N-m}$
$\large{ A, B, C, D }$ = point of intrest on frame	-	-
$\large{ L }$ = span length under consideration	$\large{in}$	$\large{mm}$
$\large{ P }$ = total consideration load	$\large{lbf}$	$\large{N}$
$\large{ R }$ = vertical reaction load at bearing point	$\large{lbf}$	$\large{N}$