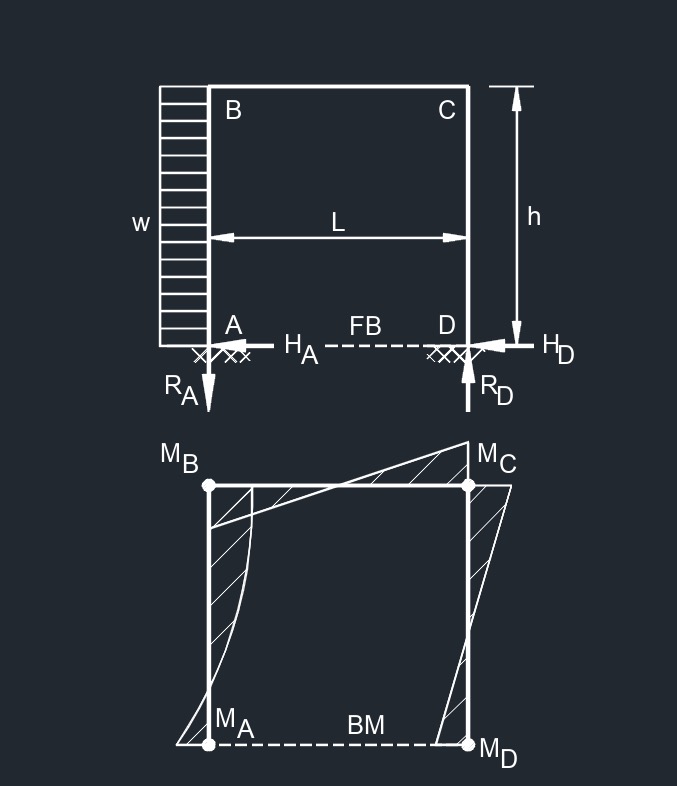
Three Member Frame - Fixed/Fixed Side Uniformly Distributed Load
Article Links |
Three Member Frame - Fixed/Fixed Side Uniformly Distributed Load formulas
Needed Values |
|
| \(\large{ e = \frac{h}{L} }\) | |
| \(\large{ \beta = \frac{I_h}{I_v} }\) | |
Support Reactions |
|
| \(\large{ R_A = R_D = \frac{ w\;h\; \beta\; e^2 }{ 6\; \beta \;e\;+\;1 } }\) | |
| \(\large{ H_A = \frac{w\;h}{4} \; \left( \frac{8\; \beta\;e\;+\;17 }{2\; \left( \beta\;e\;+\;2 \right) } - \frac{4\; \beta\;e\;+\;3 }{6\; \beta\;e\;+\;1 } \right) }\) | |
| \(\large{ H_D = \frac{w\;h}{4} \; \left( \frac{4\; \beta\;e\;+\;3 }{6\; \beta\;e\;+\;1 } - \frac{1 }{2\; \left( \beta\;e\;+\;2 \right) } \right) }\) | |
Bending Moments |
|
| \(\large{ M_A = \frac{w\;h^2}{4} \; \left( \frac{4\; \beta\;e\;+\;1 }{6\; \beta\;e\;+\;1 } + \frac{\beta \;e \;+\; 3 }{6\; \left( \beta\;e\;+\;2 \right) } \right) }\) | |
| \(\large{ M_B = \frac{w\;h^2 \; \beta \;e}{4} \; \left( \frac{ 6 }{6\; \beta\;e\;+\;1 } - \frac{ 1 }{6\; \left( \beta\;e\;+\;2 \right) } \right) }\) | |
| \(\large{ M_C = \frac{w\;h^2 \; \beta \;e}{4} \; \left( \frac{ 2 }{6\; \beta\;e\;+\;1 } - \frac{ 1 }{6\; \left( \beta\;e\;+\;2 \right) } \right) }\) | |
| \(\large{ M_D = \frac{w\;h^2}{4} \; \left( \frac{4\; \beta\;e\;+\;1 }{6\; \beta\;e\;+\;1 } - \frac{\beta \;e \;+\; 3 }{6\; \left( \beta\;e\;+\;2 \right) } \right) }\) |
Where:
| Units | English | Metric |
| \(\large{ h }\) = height of frame | \(\large{in}\) | \(\large{mm}\) |
| \(\large{ H }\) = horizontal reaction load at bearing point | \(\large{lbf}\) | \(\large{N}\) |
| \(\large{ I_h }\) = horizontal member second moment of area (moment of inertia) | \(\large{in^4}\) | \(\large{mm^4}\) |
| \(\large{ I_v }\) = vertical member second moment of area (moment of inertia) | \(\large{in^4}\) | \(\large{mm^4}\) |
| \(\large{ w }\) = load per unit length | \(\large{\frac{lbf}{in}}\) | \(\large{\frac{N}{m}}\) |
| \(\large{ M }\) = maximum bending moment | \(\large{lbf-in}\) | \(\large{N-mm}\) |
| \(\large{ A, B, C, D, E }\) = point of intrest on frame | - | - |
| \(\large{ L }\) = span length under consideration | \(\large{in}\) | \(\large{mm}\) |
| \(\large{ R }\) = vertical reaction load at bearing point | \(\large{lbf}\) | \(\large{N}\) |
diagrams
- Bending moment diagram (BMD) - Used to determine the bending moment at a given point of a structural element. The diagram can help determine the type, size, and material of a member in a structure so that a given set of loads can be supported without structural failure.
- Free body diagram (FBD) - Used to visualize the applied forces, moments, and resulting reactions on a structure in a given condition.
- Shear force diagram (SFD) - Used to determine the shear force at a given point of a structural element. The diagram can help determine the type, size, and material of a member in a structure so that a given set of loads can be supported without structural failure.
- Uniformly distributed load (UDL) - A load that is distributed evenly across the entire length of the support area.