Inductance Formula |
||
|
\( L \;=\; \dfrac{ n^2 \cdot \mu \cdot A }{ l }\) (Inductance) \( n \;=\; \dfrac{ L \cdot l }{ 2 \cdot \mu \cdot A }\) \( \mu \;=\; \dfrac{ L \cdot l }{ n \cdot 2 \cdot A }\) \( A \;=\; \dfrac{ L \cdot l }{ n \cdot 2 \cdot \mu }\) \( l \;=\; \dfrac{ n^2 \cdot \mu \cdot A }{ L }\) |
||
| Symbol | English | Metric |
| \(\ L \) = Inductance | \(H\) | \(H\) |
| \( n \) = Number of Turns of the Coil | \(dimensionless\) | \(dimensionless\) |
| \( \mu \) (Greek symbol mu) = Permeability | \(ft^2\) | \(m^2\) |
| \( A \) = Area Encircled by the Coil | \(in^2\) | \(mm^2\) |
| \( l \) = Coil Length | \(in\) | \(mm\) |
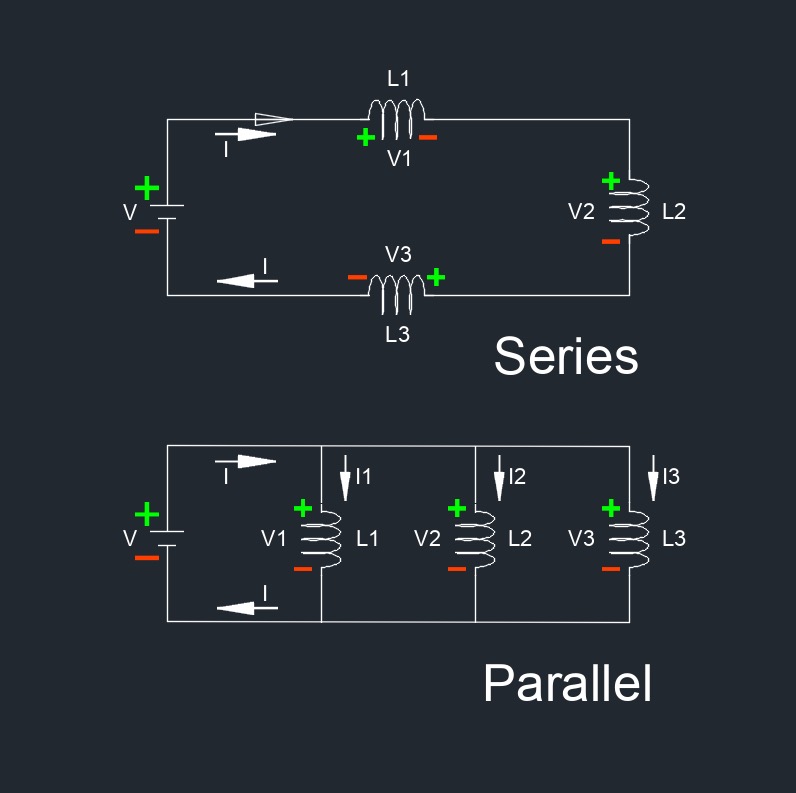Inductance, abbreviated as L, is a property of an electrical circuit or component that stores energy in a magnetic field when an electric current flows through it. Inductance is primarily associated with inductors, which are passive electronic components specifically designed to provide inductance. An inductor typically consists of a coil of wire wound around a core, which may be made of a magnetic material. When a current flows through the coil, a magnetic field is generated around it, and energy is stored in this magnetic field.
The inductance of an inductor depends on factors such as the number of turns in the coil, the size and shape of the coil, and the magnetic properties of the core material. It is directly proportional to the number of turns in the coil and the magnetic permeability of the core material.
