Spring Constant
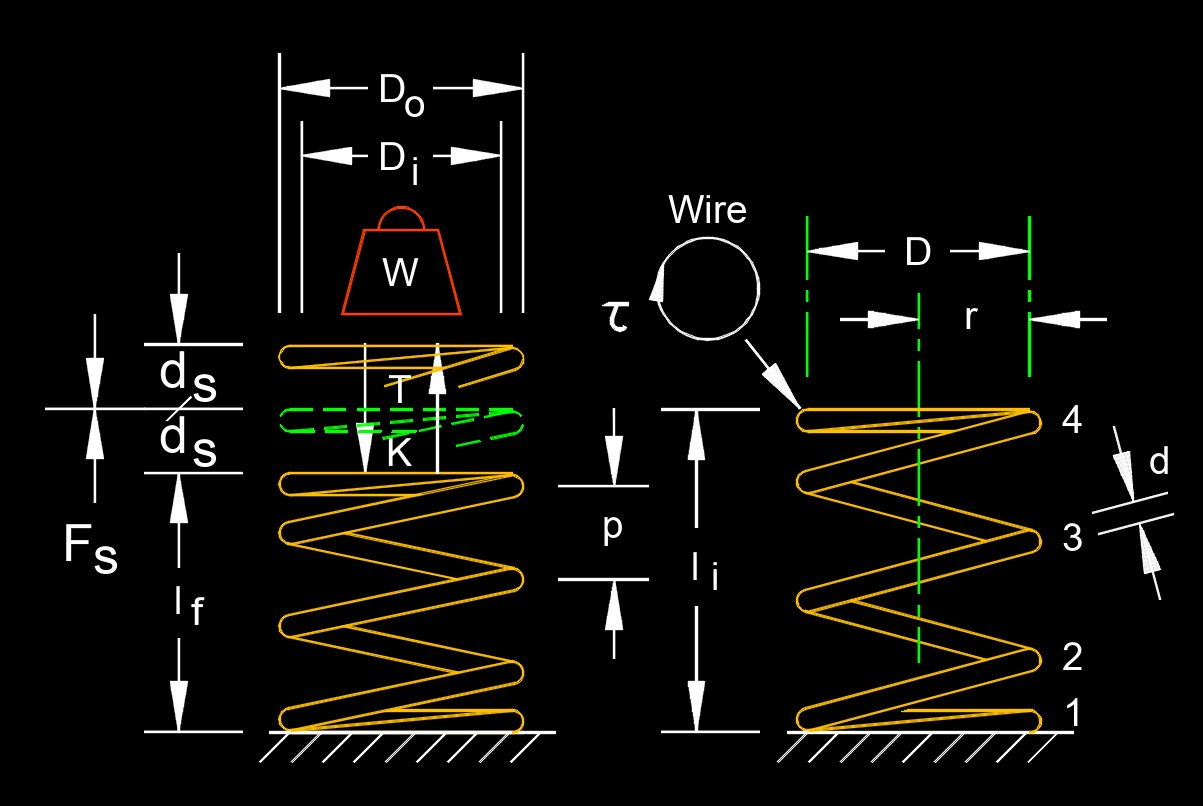 Spring constant, abbreviated as \(k_s\), also called spring force constant, is the stiffness or elasticity of a spring. It is a measure of how much force is required to stretch or compress a spring by a certain amount. Hooke's law states that the force exerted by a spring is directly proportional to the amount it is stretched or compressed from its equilibrium position, with the spring constant determining the proportionality constant. A higher spring constant indicates a stiffer spring, meaning it requires more force to produce a given displacement, while a lower spring constant indicates a softer spring, requiring less force for the same displacement.
Spring constant, abbreviated as \(k_s\), also called spring force constant, is the stiffness or elasticity of a spring. It is a measure of how much force is required to stretch or compress a spring by a certain amount. Hooke's law states that the force exerted by a spring is directly proportional to the amount it is stretched or compressed from its equilibrium position, with the spring constant determining the proportionality constant. A higher spring constant indicates a stiffer spring, meaning it requires more force to produce a given displacement, while a lower spring constant indicates a softer spring, requiring less force for the same displacement.
The spring constant is an essential parameter in various engineering and physics applications, including designing suspension systems, analyzing oscillatory systems, and understanding the behavior of materials with elastic properties.
Spring Constant formula |
||
|
\( k_s \;=\; - \;F \; d_s \) (Spring Constant) \( F \;=\; - \;( k_s \;/\; d_s ) \) \( d_s \;=\; - \;( k_s \;/\; F ) \) |
||
| Symbol | English | Metric |
| \( k_s \) = Spring Force Constant | \(lbf\) | \(N\) |
| \( F \) = Spring Force | \(lbf\) | \(N\) |
| \( d_s \) = Spring Displacement | \(in\) | \(mm\) |


