Right Pentagonal Pyramid
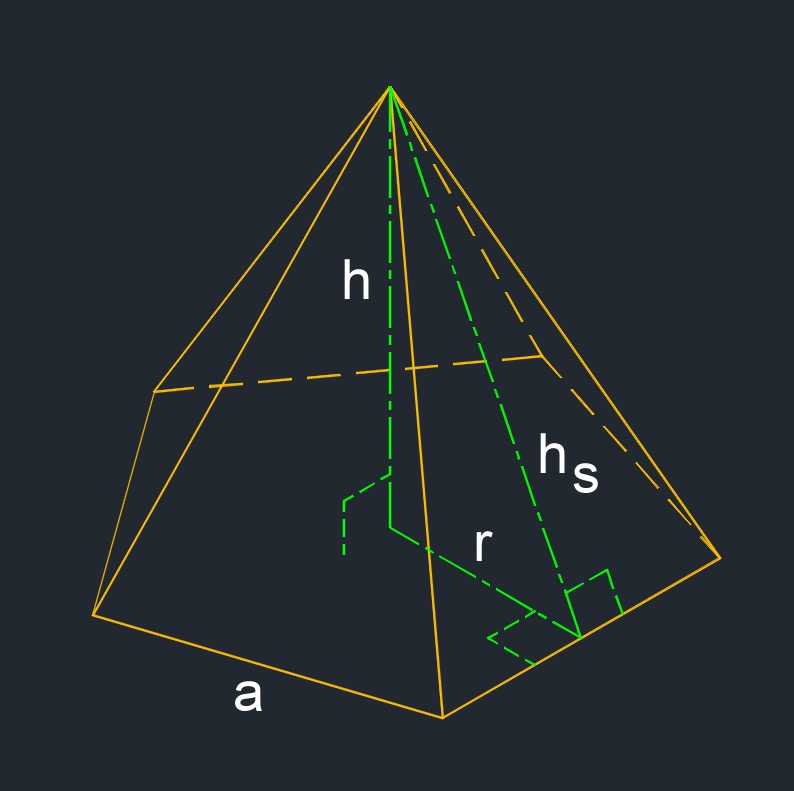
Right pentagonal pyramid (a three-dimensional figure) has pentagon base and the apex alligned above the center of the base.- 1 base
- 10 edges
- 5 faces
- 6 vertexs
Right Pentagonal Pyramid Index
- Base Area of a Right Pentagonal Pyramid
- Edge of a Right Pentagonal Pyramid
- Height of a Right Pentagonal Pyramid
- Face Area of a Right Pentagonal Pyramid
- Surface Area of a Right Pentagonal Pyramid
- Volume of a Right Pentagonal Pyramid
Base Area of a Right Pentagonal Pyramid formula |
||
| \(\large{ A_b = \frac{5}{4}\; tan\;54° \;a^2 }\) | ||
| Symbol | English | Metric |
| \(\large{ A_b }\) = base area | \(\large{ in^2 }\) | \(\large{ mm^2 }\) |
| \(\large{ a }\) = edge | \(\large{ in }\) | \(\large{ mm }\) |
| \(\large{ tan }\) = tangent | \(\large{ deg }\) | \(\large{ rad }\) |
Edge of a Right Pentagonal Pyramid formulas |
||
|
\(\large{ a = 2 \sqrt { \frac {A_s ^2}{ 75\;h^2 \;-\;25 \; \sqrt {5} \; h^2 \;+\; A_s \; \sqrt { {200 \;-\;} \sqrt {8000} } } \; \sqrt { {3 \;-\;} \sqrt {5} } } }\) \(\large{ a = \left( 5 - \sqrt 5 \right) ^{1/4} \; \sqrt { \sqrt {10}\; \frac {A_b}{5} - \sqrt {2}\; \frac {A_b} {5} } }\) \(\large{ a = \sqrt { 24 \;\frac { V } { 5\;h \;\left( \sqrt 2 \;+\; \sqrt {10} \right) } } \; { \left( 5- \sqrt 5 \right)^{1/4} } }\) |
||
| Symbol | English | Metric |
| \(\large{ a }\) = edge | \(\large{ in }\) | \(\large{ mm }\) |
| \(\large{ h }\) = height | \(\large{ in }\) | \(\large{ mm }\) |
| \(\large{ A_b }\) = base area | \(\large{ in^2 }\) | \(\large{ mm^2 }\) |
| \(\large{ A_s }\) = surface area | \(\large{ in^2 }\) | \(\large{ mm^2 }\) |
| \(\large{ V }\) = volume | \(\large{ in^3 }\) | \(\large{ mm^3 }\) |
Height of a Right Pentagonal Pyramid formulas |
||
|
\(\large{ h = 24V \frac { \sqrt { {5 \;-\;} \sqrt {5} } }{ 5\;a^2 \;\left( \sqrt {2} \;+\; \sqrt {10} \right) } }\) \(\large{ h = \sqrt{\sqrt{\frac{1}{500}} + \frac{3}{50}} \; \sqrt{ 6\;\left(\frac{A_s}{a}\right)^2 - \sqrt{20}\;\left(\frac{A_s}{a}\right)^2 - A\; \sqrt{50 - \sqrt{500} } } }\) |
||
| Symbol | English | Metric |
| \(\large{ h }\) = height | \(\large{ in }\) | \(\large{ mm }\) |
| \(\large{ a }\) = edge | \(\large{ in }\) | \(\large{ mm }\) |
| \(\large{ A_s }\) = surface area | \(\large{ in^2 }\) | \(\large{ mm^2 }\) |
| \(\large{ V }\) = volume | \(\large{ in^3 }\) | \(\large{ mm^3 }\) |
Face Area of a Right Pentagonal Pyramid formula |
||
| \(\large{ A_f = \frac{a}{2}\; \sqrt{ h^2 + \left( \frac{ a\; tan\; 54° }{2} \right) ^2 } }\) | ||
| Symbol | English | Metric |
| \(\large{ A_f }\) = face area | \(\large{ in^2 }\) | \(\large{ mm^2 }\) |
| \(\large{ a }\) = edge | \(\large{ in }\) | \(\large{ mm }\) |
| \(\large{ h }\) = height | \(\large{ in }\) | \(\large{ mm }\) |
| \(\large{ tan }\) = tangent | \(\large{ deg }\) | \(\large{ rad }\) |
Surface Area of a Right Pentagonal Pyramid formulas |
||
|
\(\large{ A_s = \frac{5}{2}\; \left( r \; a \right) + \frac{5}{2}\; \left( a \; h_s \right) }\) \(\large{ V= \frac{5}{4}\; tan\;54° \;a^2 + 5 \; \frac{a}{2} \; \sqrt{ h^2 + \left( \frac{a\; tan\; 54°}{2} \right) ^2 } }\) |
||
| Symbol | English | Metric |
| \(\large{ A_s }\) = surface area | \(\large{ in^2 }\) | \(\large{ mm^2 }\) |
| \(\large{ a }\) = edge | \(\large{ in }\) | \(\large{ mm }\) |
| \(\large{ h_s }\) = height side | \(\large{ in }\) | \(\large{ mm }\) |
| \(\large{ r }\) = radius | \(\large{ in }\) | \(\large{ mm }\) |
Volume of a Right Pentagonal Pyramid formulas |
||
|
\(\large{ V= \frac{5}{6}\; r\;a\;h }\) \(\large{ V= \frac{5}{12}\; tan\;54° \;a^2\;h }\) |
||
| Symbol | English | Metric |
| \(\large{ V }\) = volume | \(\large{ in }\) | \(\large{ mm }\) |
| \(\large{ a }\) = edge | \(\large{ in }\) | \(\large{ mm }\) |
| \(\large{ h }\) = height | \(\large{ in }\) | \(\large{ mm }\) |
| \(\large{ tan }\) = tangent | \(\large{ in }\) | \(\large{ mm }\) |
Tags: Solid Pyramid