Alternating Current

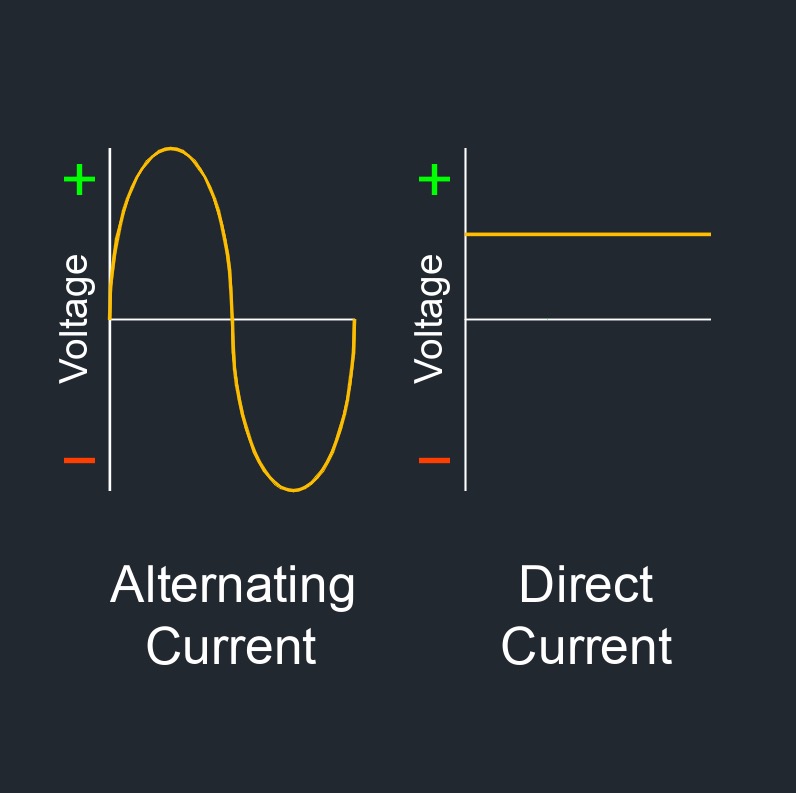Alternating current, abbreviated as AC, is an electric current that periodically reverses direction, typically at a rate of 50 or 60 cycles per second (Hz).  This reversal of direction produces a sinusoidal waveform that can be used to transmit electrical power over long distances.  AC is generated by electrical generators, which produce a voltage that alternates in polarity.  This voltage is then transmitted through power lines to homes and businesses, where it is used to power electrical devices such as lights, appliances, and electronics.

One of the advantages of AC is that it is more efficient to transmit over long distances than direct current (DC), due to the ability to use transformers to step up or step down the voltage.  This allows for high voltage transmission, which reduces the amount of energy lost due to resistance in the transmission lines.  AC is also used in many electronic devices, such as computers and televisions, as the internal components typically operate on DC power.  AC power is converted to DC power through the use of rectifiers or power supplies.

AC is an important form of electric current that is used to power a wide range of devices and systems.  Its ability to be efficiently transmitted over long distances has made it the standard for electric power distribution around the world.

 

Basic Electric Formulas \(V\) = Voltage  -  \(I\) = Amps  -  \(PF\) = Power Factor  -  \(\eta\) = Efficiency  -  \(HP\) = Horsepower
To Find	Direct Current	Alternating Current
		Single Phase	Two Phase Four Wire	Three Phase
Amperes when HP is known	\(\large{\frac{ HP \; 746 }{ V \; \%Eff } }\)	\(\large{\frac{ HP \; 746 }{ V \; \%\eta \; PF } }\)	\(\large{\frac{ HP \; 746 }{ V \; \%\eta \; PF \; 2 } }\)	\(\large{\frac{ HP \; 746 }{ V \; \%\eta \; PF \; 1.73 } }\)
Ampere when kW is known	\(\large{\frac{ kW \; 1000 }{ V } }\)	\(\large{\frac{ kW \; 1000 }{ V \; PF } }\)	\(\large{\frac{ kW \; 1000 }{ V \; PF \; 2 } }\)	\(\large{\frac{ kW \; 1000 }{ V \; PF \; 1.73 } }\)
Amperes when kVA is known	-	\(\large{\frac{ kVA \;\; 1000 }{ V } }\)	\(\large{\frac{ kVA \;\; 1000 }{ 2 \; V } }\)	\(\large{\frac{ kVA \;\; 1000 }{ 1.73 \;V } }\)
Kilowatts	\(\large{\frac{ V \; I }{ 1000 } }\)	\(\large{\frac{ V \; I \; PF }{ 1000 } }\)	\(\large{\frac{ V \; I \; PF \; 2 }{ 1000 } }\)	\(\large{\frac{ V \; I \; PF \; 1.732 }{ 1000 } }\)
Kilovolt Amperes kVA	-	\(\large{\frac{ V \; I }{ 1000 } }\)	\(\large{\frac{ V \; I \; 2 }{ 1000 } }\)	\(\large{\frac{ V \; I \; 1.732 }{ 1000 } }\)
Horsepower	\(\large{\frac{ V \; I \; \%\eta }{ 746 } }\)	\(\large{\frac{ V \; I \; \%\eta \; PF }{ 746 } }\)	\(\large{\frac{ V \; I \; \%\eta \; PF \; 2 }{ 746 } }\)	\(\large{\frac{ V \; I \; \%\eta \; PF \; 1.73 }{ 746 } }\)