Magnetic Flux
Magnetic Flux Formula |
||
|
\( \Phi_B \;=\; B \cdot A \) (Magnetic Flux) \( B \;=\; \dfrac{ \Phi_B }{ A } \) \( A \;=\; \dfrac{ \Phi_B }{ B } \) |
||
| Symbol | English | Metric |
| \( \Phi_B \) (Greek symbol Phi) = Magnetic Flux | \(Vs\) | \(Wb\) |
| \( B \) = Magnetic Field | \( G\) | \( T\) |
| \( A \) = Area Cross-section Perpendicular to Magnetic Field B | \(in^2\) | \(m^2\) |
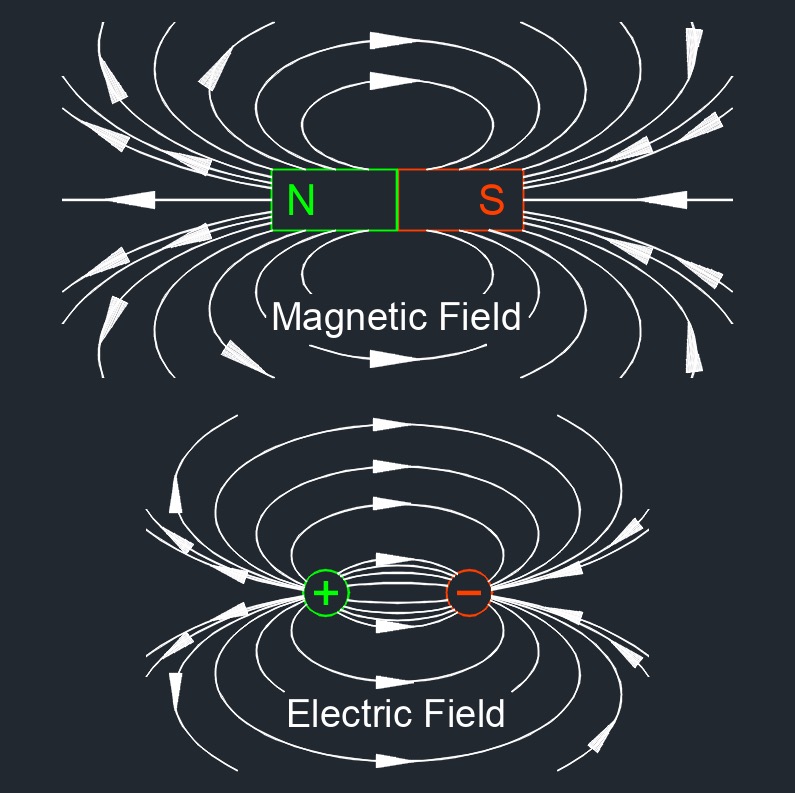 Magnetic flux, abbreviated as \(\Phi\) or \(\Phi_B\), is a measure of the total magnetic field that passes through a given area. The magnetic flux through a surface is defined mathematically as the product of the magnetic field passing through the surface and the surface area itself. Magnetic flux is a method that can detect wall thickness from corrosion and pitting without affecting the pipe. The magnetic flux through some surface is porportional to the number of field lines passing through that surface. This is essential in understanding electromagnetic induction, Faraday's law, and other phenomena related to the interaction between magnetic fields and electric circuits.
Magnetic flux, abbreviated as \(\Phi\) or \(\Phi_B\), is a measure of the total magnetic field that passes through a given area. The magnetic flux through a surface is defined mathematically as the product of the magnetic field passing through the surface and the surface area itself. Magnetic flux is a method that can detect wall thickness from corrosion and pitting without affecting the pipe. The magnetic flux through some surface is porportional to the number of field lines passing through that surface. This is essential in understanding electromagnetic induction, Faraday's law, and other phenomena related to the interaction between magnetic fields and electric circuits.
Magnetic Flux Formula |
||
|
\( \Phi_B \;=\; B \cdot A \cdot cos(\theta) \) (Magnetic Flux) \( B \;=\; \dfrac{ \Phi_B }{ A \cdot cos(\theta) } \) \( A \;=\; \dfrac{ \Phi_B }{ B \cdot cos(\theta) } \) \( cos\;\theta \;=\; \dfrac{ \Phi_B }{ B \cdot A } \) |
||
| Symbol | English | Metric |
| \( \Phi_B \) (Greek symbol Phi) = Magnetic Flux | \(Vs\) | \(Wb\) |
| \( B \) = Magnetic Field | \( G\) | \( T\) |
| \( A \) = Area Cross-section Perpendicular to Magnetic Field B | \(in^2\) | \(m^2\) |
| \( \theta \) = Angle Between a Perpendicular Vector to the Area and the Magnetic Field | \(deg\) | \(rad\) |
The orientation of the magnetic field lines with respect to the surface through which the magnetic flux is being measured is a factor in determining the magnetic flux. The angle θ in the magnetic flux formula (Φ = B * A* cos (θ)) represents the angle between the magnetic field lines and the normal to the surface.
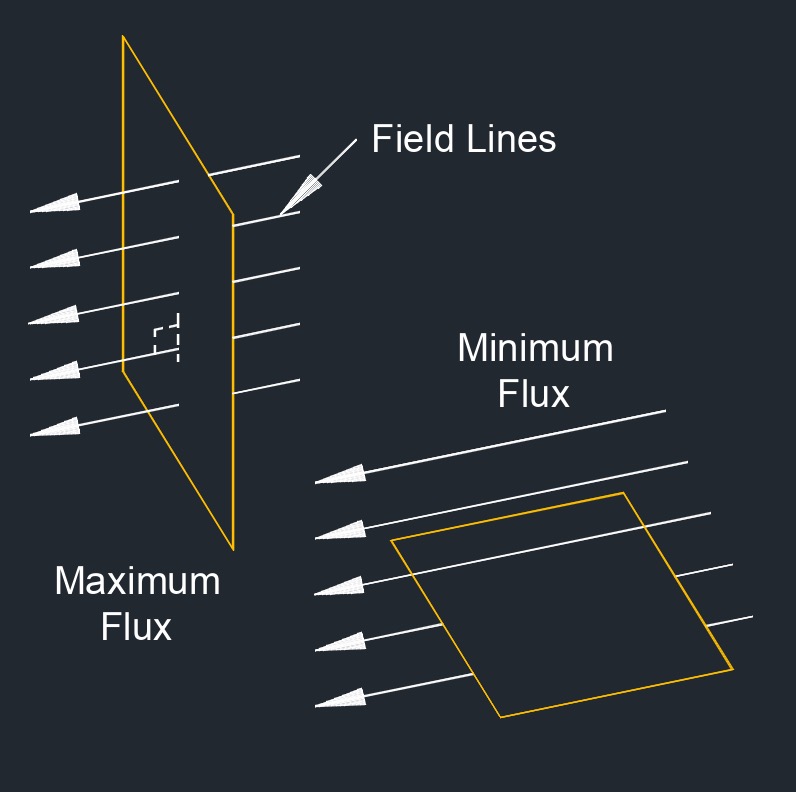
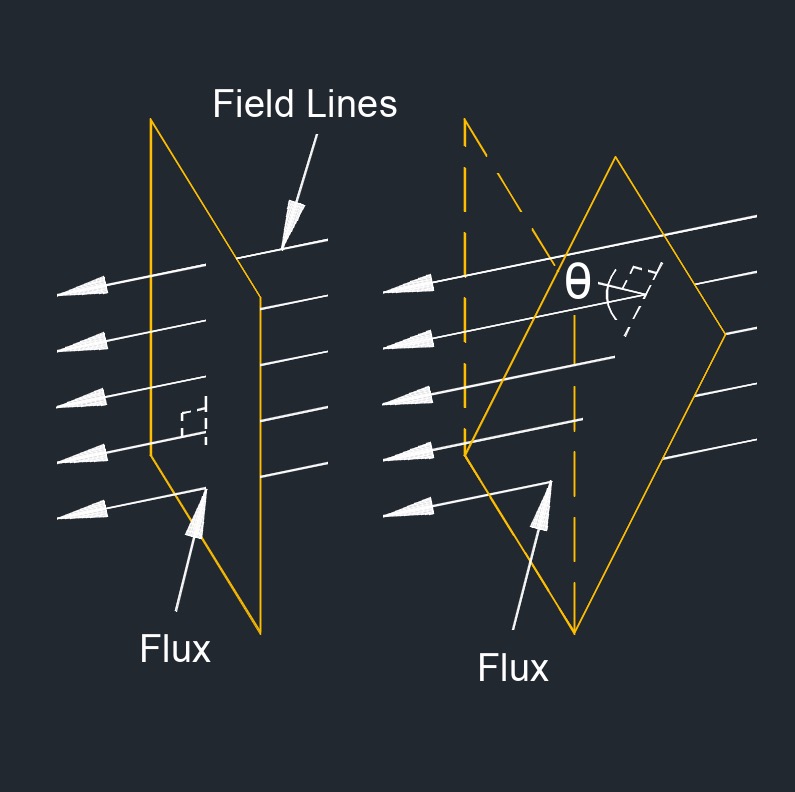
Here's How the Orientation Affects the Magnetic Flux
Maximum Flux (θ = 0) - When the surface is parallel to the magnetic field lines (θ = 0), the magnetic flux is maximized. In this case, cos (0) = 1, and the formula simplifies to Φ = B * A. This is because the magnetic field lines are penetrating the surface perpendicularly, maximizing the magnetic flux.
Zero Flux (θ = 90) - When the surface is perpendicular to the magnetic field lines (θ = 90), the magnetic flux is zero. In this case, cos (90) = 0, and the formula becomes Φ = B * A * 0 = 0. This happens because none of the magnetic field lines are passing through the surface.
Intermediate Angles (0 < θ < 90) - For angles between 0 and 90 degrees, the magnetic flux is proportional to the component of the magnetic field perpendicular to the surface. As the angle increases from 0 to 90 degrees, the component of the magnetic field perpendicular to the surface decreases, leading to a reduction in the magnetic flux.
Understanding the orientation of the magnetic field lines is crucial in various applications, such as electromagnetic induction, where changes in magnetic flux induce an electromotive force (EMF) in a coil or conductor according to Faraday's law of electromagnetic induction.

