Linear Thermal Expansion Formula |
||
|
\( \overrightarrow{\Delta l} \;=\; l_f - l_i \) (Linear Thermal Expansion) \( l_f \;=\; \overrightarrow{\Delta l} + l_i \) \( l_i \;=\; l_f - \overrightarrow{\Delta l} \) |
||
| Symbol | English | Metric |
| \(\large{ \overrightarrow{\Delta l} }\) = linear thermal expansion | \(in \;/\; in\;F\) | \(mm \;/\; mm\;C\) |
| \(\large{ l_f }\) = final length | \(ft\) | \(m\) |
| \(\large{ l_i }\) = initial length | \(ft\) | \(m\) |
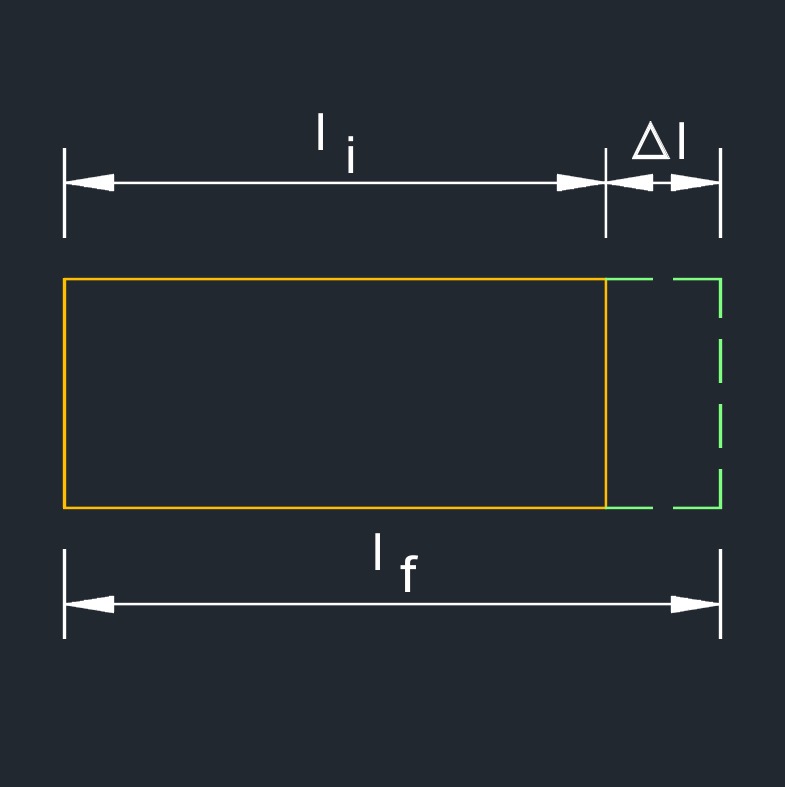Linear thermal expansion, abbreviated as \(\Delta l\), also known as line thermal expansion, is a porportional change in the origional length and change in temperature due to the heating or cooling of an object. When a substance is heated, its molecules or particles gain kinetic energy and vibrate more vigorously, leading to an increase in the average separation between them. This increase in molecular spacing causes the material to expand in length or dimension.
Linear Thermal Expansion Formula |
||
|
\( \overrightarrow{\Delta l} \;=\; \overrightarrow{\alpha_l} \cdot l_i \cdot \Delta T \) (Linear Thermal Expansion) \( \overrightarrow{\alpha_l} \;=\; \dfrac{ \overrightarrow{\Delta l} }{ l_i \cdot \Delta T }\) \( l_i \;=\; \dfrac{ \overrightarrow{\Delta l} }{ \overrightarrow{\alpha_l} \cdot \Delta T }\) \( \Delta T \;=\; \dfrac{ \overrightarrow{\Delta l} }{ \overrightarrow{\alpha_l} \cdot l_i }\) |
||
| Symbol | English | Metric |
| \( \overrightarrow{\Delta l} \) = linear thermal expansion | \(in \;/\; in\;F\) | \(mm \;/\; mm\;C\) |
| \( \overrightarrow{\alpha_l} \) (Greek symbol alpha) = linear thermal expansion coefficient | \(in \;/\; in\;F\) | \(mm \;/\; mm\;C\) |
| \( l_i \) = initial length | \(ft\) | \(m\) |
| \( \Delta T \) = temperature change | \(F\) | \(C\) |
The linear thermal expansion coefficient is typically positive, indicating that most materials expand when heated. However, there are exceptions, such as certain materials with negative thermal expansion coefficients that contract when heated. The coefficient varies for different materials and depends on their atomic or molecular structure. For example, metals generally have higher thermal expansion coefficients compared to nonmetals.
It is an important consideration in engineering, construction, and materials science. It affects the dimensional stability and integrity of structures and materials exposed to temperature changes. Understanding and accounting for linear thermal expansion is crucial to ensure proper fit, avoid unwanted stresses or deformations, and design systems that can accommodate the dimensional changes associated with temperature variations.
