Linear Thermal Restrained Expansion
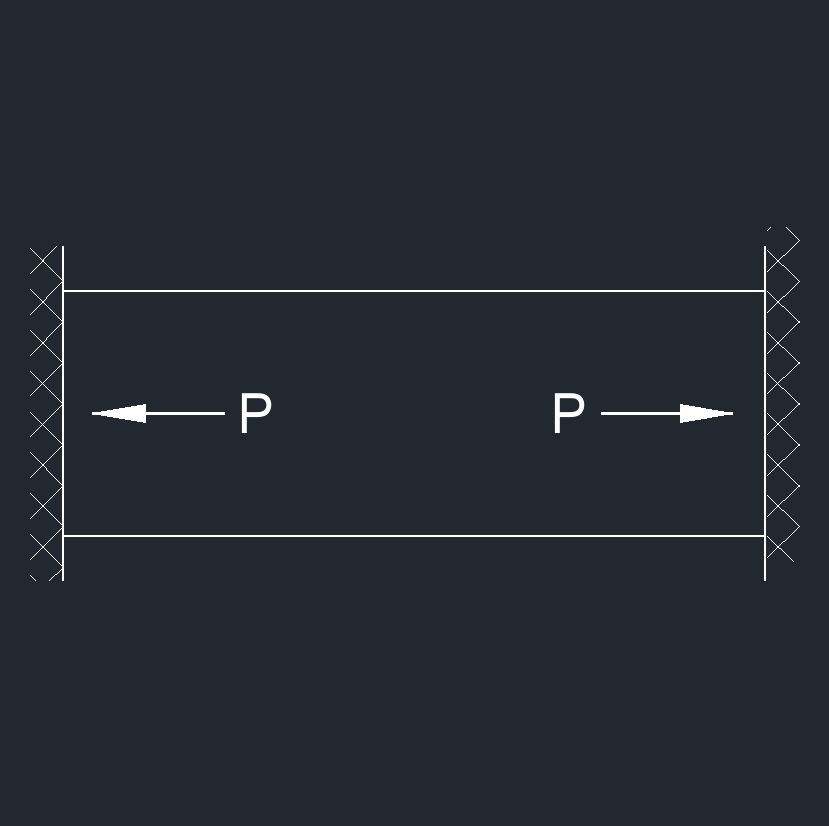Linear thermal restrained expansion is where an object or material experiences expansion due to an increase in temperature, but this expansion is limited or restrained by external factors or constraints. This is often encountered in structures or systems where thermal expansion needs to be controlled or restricted. When a material is heated, its molecules gain energy and move more rapidly, leading to an increase in volume or dimensions. However, in certain situations, the expansion is prevented or restricted by the surrounding conditions. This restriction can result from physical constraints such as being attached to a rigid support or being part of a structure that prevents free expansion.
Linear thermal restrained expansion is important in engineering and construction, where precise dimensional control is crucial. For example, in bridges, buildings, or pipelines, engineers may need to design structures that allow for thermal expansion and contraction while ensuring that movements are within acceptable limits to avoid structural damage or failure. Techniques like expansion joints, flexible connectors, and careful material selection are employed to manage the effects of thermal expansion in such applications.
Linear Thermal Restrained Expansion Formula |
||
|
\( \Delta p = \lambda \; A_i \; \overrightarrow{\alpha_l} \; \Delta T \) (Linear Thermal Restrained Expansion) \( \lambda = \Delta p \;/\; A_i \; \overrightarrow{\alpha_l} \; \Delta T \) \( A_i = \Delta p \;/\; \lambda \; \overrightarrow{\alpha_l} \; \Delta T \) \( \overrightarrow{ \alpha_l } = \Delta p \;/\; \lambda \; A_i \; \Delta T \) \( \Delta T = \Delta p \;/\; \lambda \; A_i \; \overrightarrow{\alpha_l} \) |
||
| Symbol | English | Metric |
| \( \Delta p \) = pressure differential | \(lbf \;/\; in^2 \) | \(Pa \) |
| \( \lambda \) (Greek symbol lambda) = modulus of elasticity | \( lbf \;/\; in^2 \) | \(Pa \) |
| \( A_i \) = initial area of object | \( in^2 \) | \( mm^2 \) |
| \( \overrightarrow{\alpha_l} \) (Greek symbol alpha) = linear thermal expansion coefficient | \(in \;/\; in\;F\) | \(mm \;/\; mm\;C\) |
| \( \Delta T \) = temperature differential | \( F \) | \( C \) |
Linear Thermal Restrained Expansion Formula |
||
| \( \sigma_c = - ( p \;/\; A_i ) \) | ||
| Symbol | English | Metric |
| \( \sigma_c \) (Greek symbol sigma) = compressive stress | \( lbf \;/\; in^2 \) | \( Pa \) |
| \( A_i \) = initial area of object | \( in^2 \) | \( mm^2 \) |
| \( p \) = pressure | \( lbf \;/\; in^2 \) | \( Pa \) |
Linear Thermal Restrained Expansion Formula |
||
| \( \sigma_c = - \lambda\; A_i \; \overrightarrow{\alpha_l} \; \Delta T \) | ||
| Symbol | English | Metric |
| \( \sigma_c \) (Greek symbol sigma) = compressive stress | \( lbf \;/\; in^2 \) | \( Pa \) |
| \( \overrightarrow{\alpha_l} \) (Greek symbol alpha) = linear thermal expansion coefficient | \(in \;/\; in\;F\) | \(mm \;/\; mm\;C\) |
| \( A_i \) = initial area of object | \( in^2 \) | \( mm^2 \) |
| \( \lambda \) (Greek symbol lambda) = modulus of elasticity | \(lbf \;/\; in^2 \) | \( Pa \) |
| \( \Delta T \) = temperature differential | \( F \) | \( C \) |
