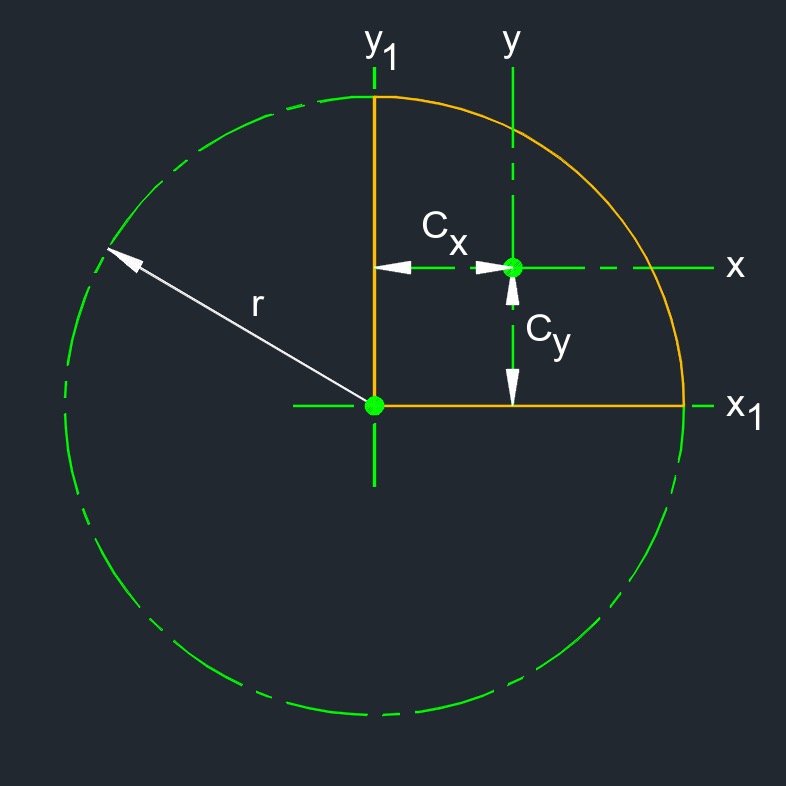
Radius of Gyration of a Quarter Circle formulas |
||
|
\( k_{x} \;=\; r \cdot \sqrt{ \dfrac{ 1 }{ 4 } - \dfrac{ 16 }{ 9 \cdot \pi^2} } \) \( k_{y} \;=\; r \cdot \sqrt{ \dfrac{ 1 }{ 4 } - \dfrac{ 16 }{ 9 \cdot \pi^2} } \) \( k_{z} \;=\; r \cdot \sqrt{ \dfrac{ 1 }{ 2 } - \dfrac{ 16 }{ 9 \cdot \pi^2} } \) \( k_{x1} \;=\; \dfrac{ r }{ 2 } \) \( k_{y1} \;=\; \dfrac{ r }{ 2 } \) \( k_{z1} \;=\; \dfrac{ \sqrt {2} }{ 2 } \cdot r \) |
||
| Symbol | English | Metric |
| \( k \) = radius of gyration | \( in \) | \( mm \) |
| \( \pi \) = Pi | \(3.141 592 653 ...\) | \(3.141 592 653 ...\) |
| \( r \) = radius | \( in \) | \( mm \) |
