Yield Strength
Yield Strength Formula |
||
|
\( \sigma \;=\; \dfrac{F}{A_c}\) (Yield Strength) \( F \;=\; \sigma \cdot A_c \) \( A_c \;=\; \dfrac{F}{ \sigma}\) |
||
| Symbol | English | Metric |
| \( \sigma \) (Greek symbol sigma) = Yield Strength | \(lbf\;/\;in^2\) | \(Pa\) |
| \( F \) = Load (Force) at the Yield Point | \( lbf \) | \( N \) |
| \( A_c \) = Origional Area Cross-section | \( in^2 \) | \( mm^2 \) |
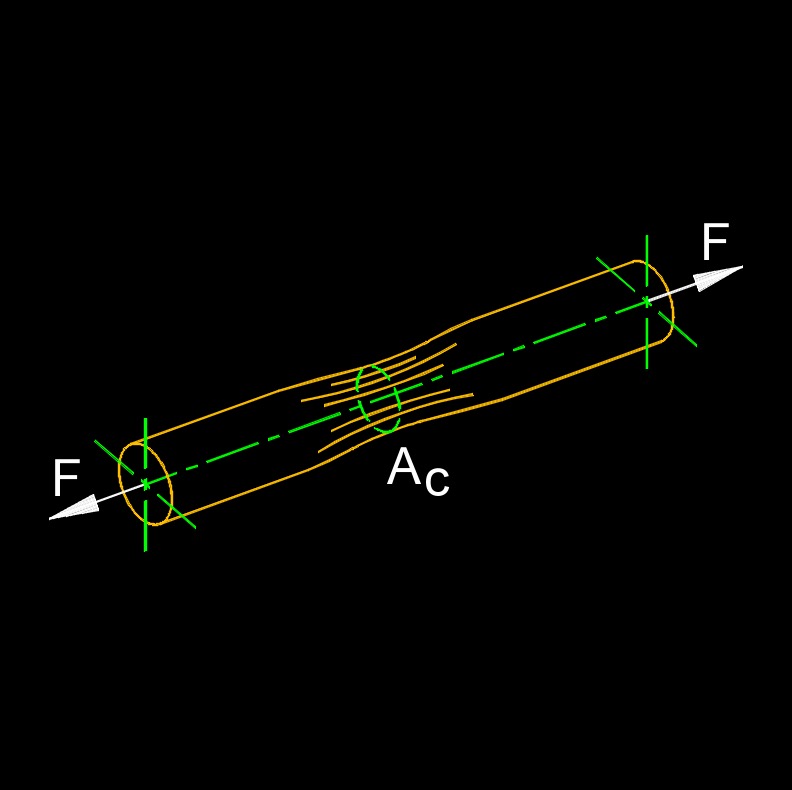 Yield strength, abbreviated as \(\sigma\) (Greek symbol sigma), also called yield stress or yield point, is the minimum stress that leads to permanent deformation of the material. It is important to note that the yield strength of a material is not a fixed value, but rather depends on various factors such as the composition, processing, and testing conditions of the material. Yield strength is a mechanical property of a material that represents the stress at which it undergoes a significant and permanent deformation, typically in the form of plastic deformation. It is an important parameter used to assess the strength and mechanical behavior of materials under load.
Yield strength, abbreviated as \(\sigma\) (Greek symbol sigma), also called yield stress or yield point, is the minimum stress that leads to permanent deformation of the material. It is important to note that the yield strength of a material is not a fixed value, but rather depends on various factors such as the composition, processing, and testing conditions of the material. Yield strength is a mechanical property of a material that represents the stress at which it undergoes a significant and permanent deformation, typically in the form of plastic deformation. It is an important parameter used to assess the strength and mechanical behavior of materials under load.
When a material is subjected to external forces or loads, it initially undergoes elastic deformation, where it deforms and stretches but returns to its original shape upon the removal of the load. However, as the applied stress increases, the material reaches a point known as the yield point or yield strength. At this point, the material begins to undergo plastic deformation, where it experiences permanent changes in shape even after the load is removed.
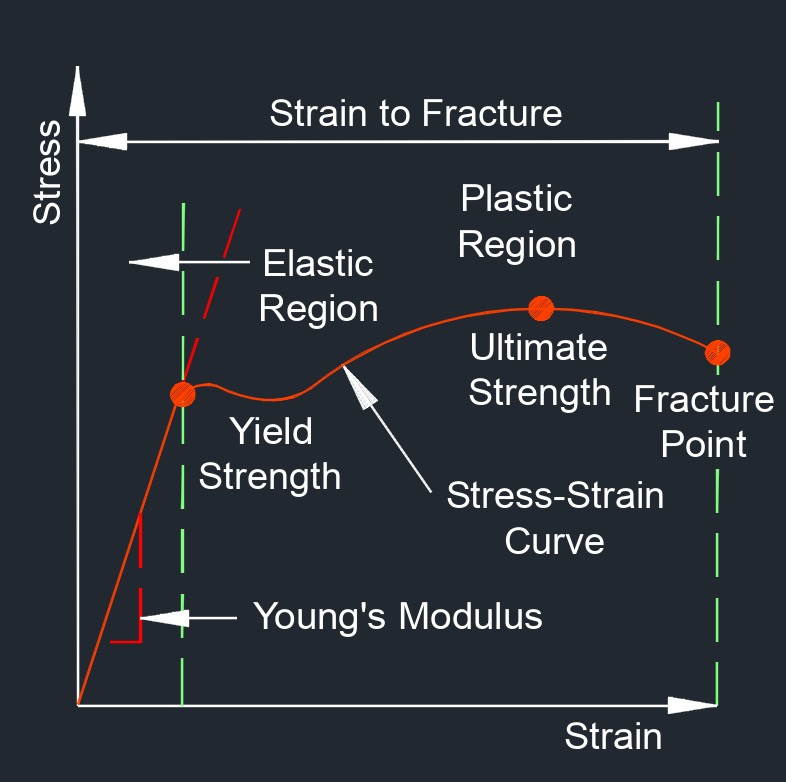 Yield strength is measured as the stress required to cause a specified amount of plastic deformation. It is typically determined through mechanical testing, such as a tensile test, where a specimen of the material is subjected to axial tension until it reaches the point of yield. The stress at which the material exhibits a specific amount of permanent deformation, often 0.2% or 0.5% of the original gauge length, is defined as the yield strength.
Yield strength is measured as the stress required to cause a specified amount of plastic deformation. It is typically determined through mechanical testing, such as a tensile test, where a specimen of the material is subjected to axial tension until it reaches the point of yield. The stress at which the material exhibits a specific amount of permanent deformation, often 0.2% or 0.5% of the original gauge length, is defined as the yield strength.
Yield strength is an important parameter in material selection, structural design, and engineering analysis. It helps engineers determine the maximum stress a material can withstand before permanent deformation occurs, enabling them to ensure the structural integrity, safety, and reliability of components and structures. Different materials exhibit different yield strengths depending on their composition, microstructure, processing, and other factors. The yield strength is an essential consideration in industries such as construction, manufacturing, aerospace, and automotive engineering, where the mechanical strength and performance of materials are critical.

