Angular Momentum for a Rigid Body
Angular Momentum for a Rigid Body Formula |
||
|
\( L \;=\; I \cdot \omega \) (Angular Momentum of a Rigid Body) \( I \;=\; \dfrac{ L }{ \omega }\) \( \omega \;=\; \dfrac{ L }{ I }\) |
||
| Symbol | English | Metric |
| \( L \) = Angular Momentum (Rotational Momentum) | \(lbm - ft^2 \;/\; sec\) | \(kg - m^2 \;/\; s\) |
| \( I \) = Moment of Inertia | \(in^4\) | \(m^4\) |
| \( \omega \) (Greek symbol omega) = Angular Velocity | \(deg \;/\; sec\) | \(rad \;/\; s\) |
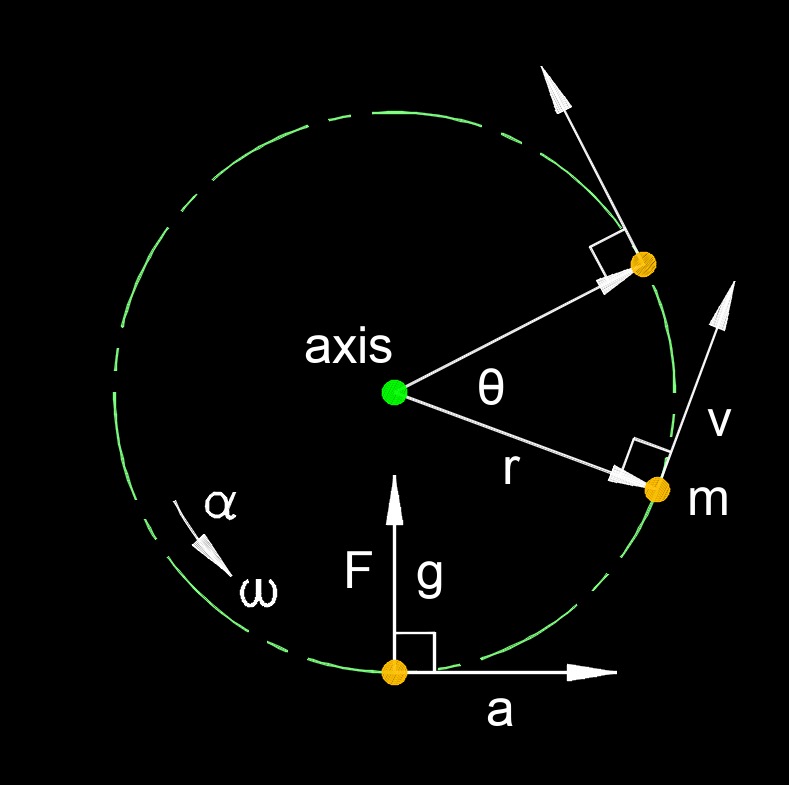
Angular momentum for a rigid body is a measure of the rotational motion of the entire object about a fixed axis or point. It represents the sum of the angular momentum of all the individual particles that make up the body. For a rigid body rotating about a fixed axis, the angular momentum depends on both the distribution of the body’s mass and its angular velocity. The direction of the angular momentum vector is along the axis of rotation, following the right-hand rule. In essence, angular momentum describes how difficult it is to change the rotational motion of a rigid body, playing a key role in the conservation of rotational dynamics.

