Volumetric Thermal Expansion Formula |
||
|
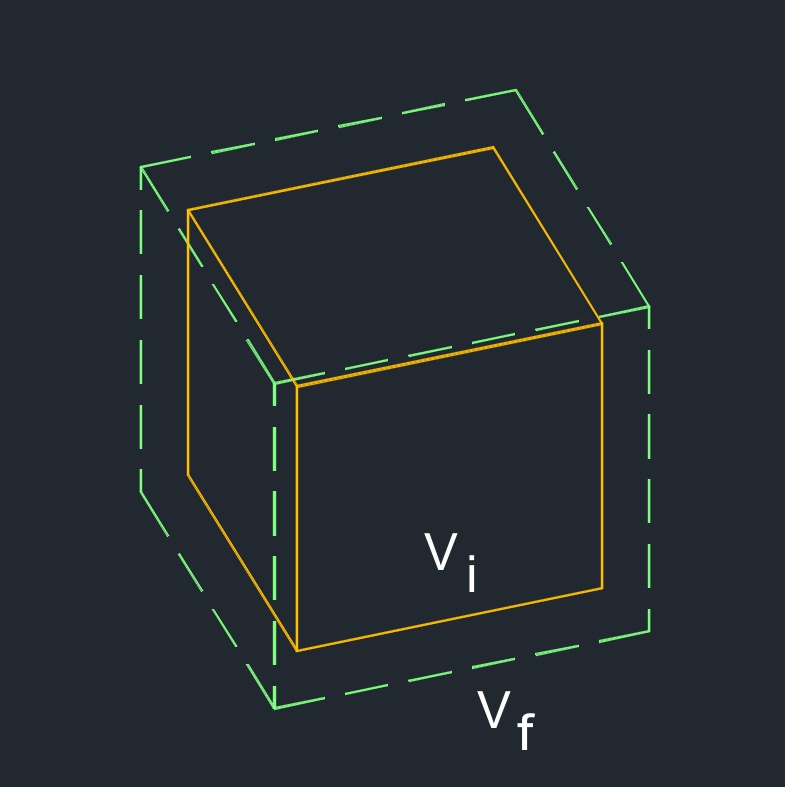
\( \Delta V \;=\; V_f - V_i \) (Volumetric Thermal Expansion) \( V_f \;=\; \Delta V + V_i \) \( V_i \;=\; V_f - \Delta V \) |
||
| Symbol | English | Metric |
| \( \Delta V \) = volumetric thermal expansion | \(in^3 \;/\; in^3\;F\) | \(mm^3 \;/\; mm^3\;C\) |
| \( V_f \) = final volume | \(in^3\) | \(mm^3\) |
| \( V_i \) = initial volume | \(in^3\) | \(mm^3\) |
Volumetric thermal expansion, abbreviated as \(\Delta V\), also called volume thermal expansion, volume expansion or linear volume thermal expansion, takes place in gasses and liquids when a change in temperature, volume or type of substance occures. When a substance is heated, its molecules or particles gain kinetic energy and tend to move more vigorously, resulting in an increase in the overall volume of the substance.
Volumetric Thermal Expansion Formula |
||
|
\( \Delta V \;=\; 3 \cdot \overrightarrow{\alpha_l} \cdot V_i \cdot \Delta T \) (Volumetric Thermal Expansion) \( \overrightarrow{\alpha_l} \;=\; \dfrac{ \Delta V }{ 3 \cdot V_i \cdot \Delta T }\) \( V_i \;=\; \dfrac{ \Delta V }{ 3 \cdot \overrightarrow{\alpha_l} \cdot \Delta T }\) \( \Delta T \;=\; \dfrac{ \Delta V }{ 3 \cdot \overrightarrow{\alpha_l} \cdot V_i }\) |
||
| Symbol | English | Metric |
| \( \Delta V \) = volumetric thermal expansion | \(in^3 \;/\; in^3\;F\) | \(mm^3 \;/\; mm^3\;C\) |
| \( \overrightarrow{\alpha_l} \) (Greek symbol alpha) = linear thermal expansion coefficient | \(in \;/\; in\;F\) | \(mm \;/\; mm\;C\) |
| \( V_i \) = initial volume | \(in^3\) | \(mm^3\) |
| \( \Delta T \) = temperature change | \(F\) | \(C\) |
Different substances have different values of the volumetric thermal expansion coefficient, which depend on the material's properties and molecular structure. Generally, most substances expand when heated, resulting in a positive value for the volumetric thermal expansion coefficient. However, some rare substances, such as water between 0°C and 4°C, exhibit anomalous behavior, where they contract upon heating.
Volumetric thermal expansion is an important consideration in engineering, materials science, and thermodynamics. It affects the behavior of structures and materials subjected to temperature changes, and it is essential for designing systems that can accommodate the dimensional changes associated with temperature variations.
Volumetric Thermal Expansion Formula |
||
|
\( V_f \;=\; V_i \cdot ( 1 + 3 \cdot \overrightarrow{\alpha_l} \cdot \Delta T ) \) (Volumetric Thermal Expansion) \( V_i \;=\; \dfrac{ V_f }{ 1 + 3 \cdot \overrightarrow{\alpha_l} \cdot \Delta T }\) \( \overrightarrow{\alpha_l} \;=\; \dfrac{ \dfrac{ V_f }{ V_i } - 1 }{ 3 \cdot \Delta T }\) \( \Delta T \;=\; \dfrac{ \dfrac{ V_f }{ V_i } - 1 }{ 3 \cdot \overrightarrow{\alpha_l} }\) |
||
| Symbol | English | Metric |
| \( V_f \) = final volume | \(in^3\) | \(mm^3\) |
| \( V_i \) = initial volume | \(in^3\) | \(mm^3\) |
| \( \overrightarrow{\alpha_l}\) (Greek symbol alpha) = linear thermal expansion coefficient | \(in \;/\; in\;F\) | \(mm \;/\; mm\;C\) |
| \( \Delta T \) = temperature change | \(F\) | \(C\) |