Flow Coefficient
Flow Coefficient Formula |
||
|
\( C_v \;=\; Q \; \sqrt{ \dfrac{ SG }{ \Delta p} } \) (Flow Coefficient) \( Q \;=\; \sqrt{ C_v^2 \cdot \dfrac{ \Delta p }{ SG } } \) \( SG \;=\; C_v^2 \cdot \dfrac{ \Delta p }{ Q^2 } \) \( \Delta p \;=\; \dfrac{ SG \cdot C_v^2 }{ Q^2 }\) |
||
| Symbol | English | Metric |
| \( C_v \) = Flow Coefficient | \( dimensionless \) | \( dimensionless \) |
| \( Q \) = Liquid Flow Rate (gpm for Liquid) | \(gal \;/\; min\) | \(L \;/\; min\) |
| \( SG \) = Liquid Specific Gravity (Water at 60°F = 1.0000) | \( dimensionless \) | \( dimensionless \) |
| \( \Delta p \) = Pressure Differential (Pressure Drop Across the Valve) (psi) | \(lbf \;/\; in^2\) | \( Pa \) |
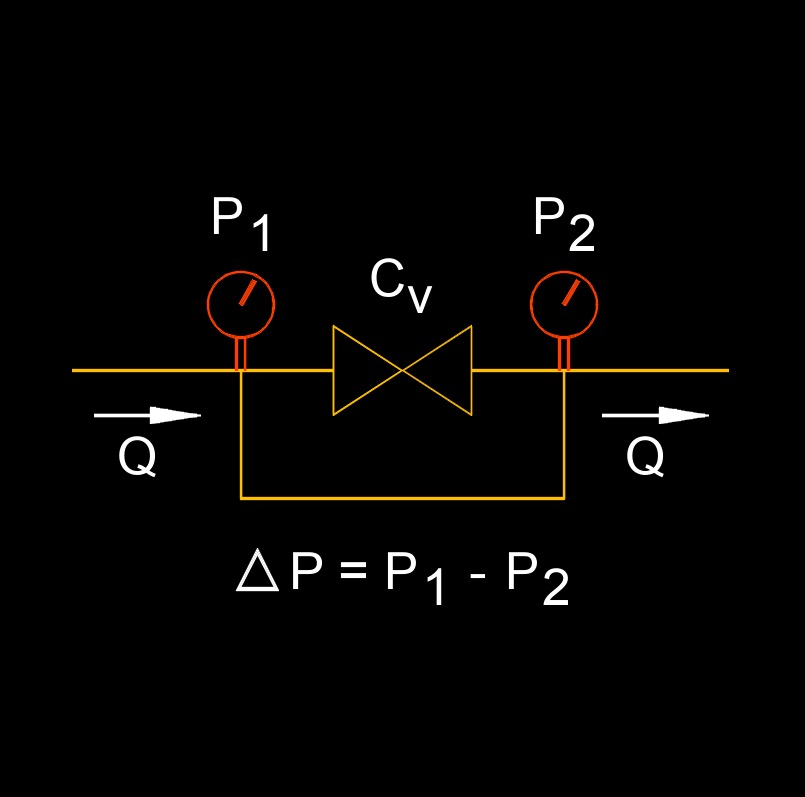 Flow coefficient, abbreviated as \(C_v\), a dimensionless number, also called valve coefficient or valve flow coefficient, can be described as the volume (in US gallons) of water at 60°F that will flow per minute through a valve with a pressure drop of 1 psi across the valve. This gives us a method to compare flow capabilities of different valves. The flow coefficient allows us to determine what size valve is required for a given application.
Flow coefficient, abbreviated as \(C_v\), a dimensionless number, also called valve coefficient or valve flow coefficient, can be described as the volume (in US gallons) of water at 60°F that will flow per minute through a valve with a pressure drop of 1 psi across the valve. This gives us a method to compare flow capabilities of different valves. The flow coefficient allows us to determine what size valve is required for a given application.
The flow coefficient is commonly used in fluid flow calculations to determine the pressure drop across a control device and the resulting flow rate. It is often provided by the manufacturer for specific valves, pumps or orifice plates, and can also be calculated experimentally using flow tests with a specific fluid and testing apparatus. Flow coefficient is primarily used when sizing control valves. However, it can be used to characterize other types of valves such as ball valves and butterfly valves.

Air and Gas Flow Coefficient Formula |
||
| \( C_v \;=\; \dfrac{ Q }{ 1360 } \cdot \sqrt{ \dfrac{ T_a \cdot SG }{ ( p_i + 15 ) \cdot \Delta p } } \) | ||
| Symbol | English | Metric |
| \( C_v \) = Air and Gas Flow Coefficient | \( dimensionless \) | \( dimensionless \) |
| \(Q \) = Air and Gas Flow Rate (SCFH for Air & Gas) | \(ft^3 \;/\; hr\) | \(m^3 \;/\; hr\) |
| \( T_a \) = Absolute Temperature \(^\circ R\) (\(^\circ R = ^\circ F + 460\)) | \( F \) | \( R \) |
| \(SG \) = Air and Gas Specific Gravity (Water at 60°F = 1.0000) | \( dimensionless \) | \( dimensionless \) |
| \( p_i \) = Inlet Pressure | \(lbf \;/\; in^2\) | \( Pa \) |
| \( \Delta p \) = Pressure Differential (Pressure Drop Across the Valve) (psi) | \(lbf \;/\; in^2\) | \( Pa \) |
Steam Flow Coefficient Formula |
||
| \( C_v \;=\; \dfrac{ Q }{ 63 } \cdot \sqrt{ \dfrac{ \upsilon }{ \Delta p} } \) | ||
| Symbol | English | Metric |
| \( C_v \) = Steam Flow Coefficient | \( dimensionless \) | \( dimensionless \) |
| \( Q \) = Steam Flow Rate (lbm/hr for Steam) | \(lbm \;/\; hr\) | \(L \;/\; hr\) |
| \( \upsilon \) (Greek symbol upsilon) = Specific Volume | \(ft^3 \;/\; lbm\) | \(m^3 \;/\; kg\) |
| \( \Delta p \) = Pressure Differential (Pressure Drop Across the Valve) (psi) | \(lbf \;/\; in^2\) | \( Pa \) |
