Law of Conservation
Law of conservation, also called conservation law, states that the total energy of an isolated system remains constant and its physical properties are conserved over time. The law of conservation is based on the principle of conservation of physical quantities. While energy and mass can change forms or be transferred, their total sum remains constant in an isolated system. This principle is rooted in the concept of conservation laws, which are fundamental principles in physics and form the basis for understanding many natural phenomena.
Law of conservation Index
- Law of Conservation of Angular Momentum
- Law of Conservation of Angular Momentum Formula
- Law of Conservation of Electric Charge
- Law of Conservation of Energy
- Law of Conservation of Linear Momentum
- Law of Conservation of Linear Momentum Formula
- Law of Conservation of Mass
- Law of Conservation of Mass Formula
- Law of Conservation of Mass-Energy
- Law of Conservation of Matter
- Law of Conservation of Mechanical Energy
- Law of Conservation of Mechanical Energy Formula
- Law of Conservation of Momentum
- Law of Conservation of Momentum Formula
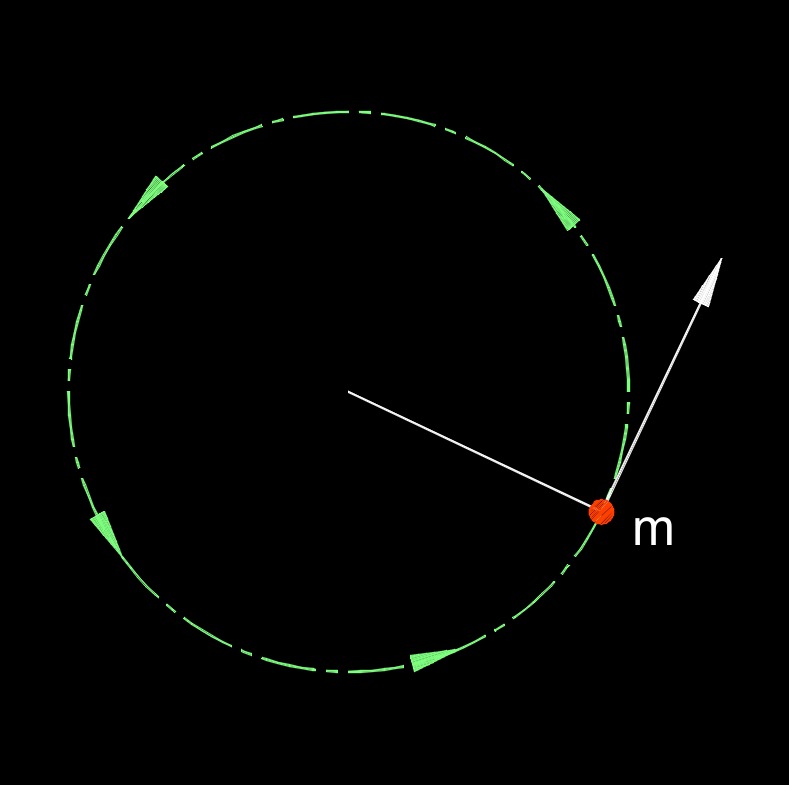Law of Conservation of Angular Momentum
Law of conservation of angular momentum states that the total angular moment of an isolated system remains constant unless acted upon by an external torque. Angular momentum is a property of rotating objects or systems and is defined as the product of moment of inertia and angular velocity.
This law can also be stated as, if no external torque acts on an isolated system, the total angular momentum of the system remains constant. In other words, the sum of the angular moment of all the objects within the system, considering their moment of inertia and angular velocity, will not change over time. An essential aspect of this law is that if one object within the system experiences an increase in angular momentum, another object or objects within the system must experience a decrease in angular momentum of an equal magnitude in order to conserve the total angular momentum of the system.
This law has numerous applications and can be observed in various physical phenomena. For example, it explains the conservation of angular momentum of spinning tops, rotating celestial bodies like planets, and even the rotational motion of subatomic particles. The conservation of angular momentum is an important principle in understanding rotational dynamics and has wide ranging implications in fields such as mechanics, astrophysics, and quantum mechanics.
law of conservation of angular momentum formula |
||
|
\( L = I \; \omega \) (Law of Conservation of Angular Momentum) \( I = L \;/\; \omega \) \( \omega = L \;/\; I \) |
||
| Symbol | English | Metric |
| \( L \) = angular momentum (rotational momentum) | \(lbm-ft^2\;/\;sec\) | \(kg-m^2\;/\;s\) |
| \( I \) = moment of inertia | \(in^4 \) | \(mm^4 \) |
| \( \omega \) (Greek symbol omega) = angular velocity | \(deg\;/\;sec\) | \(rad\;/\;s\) |
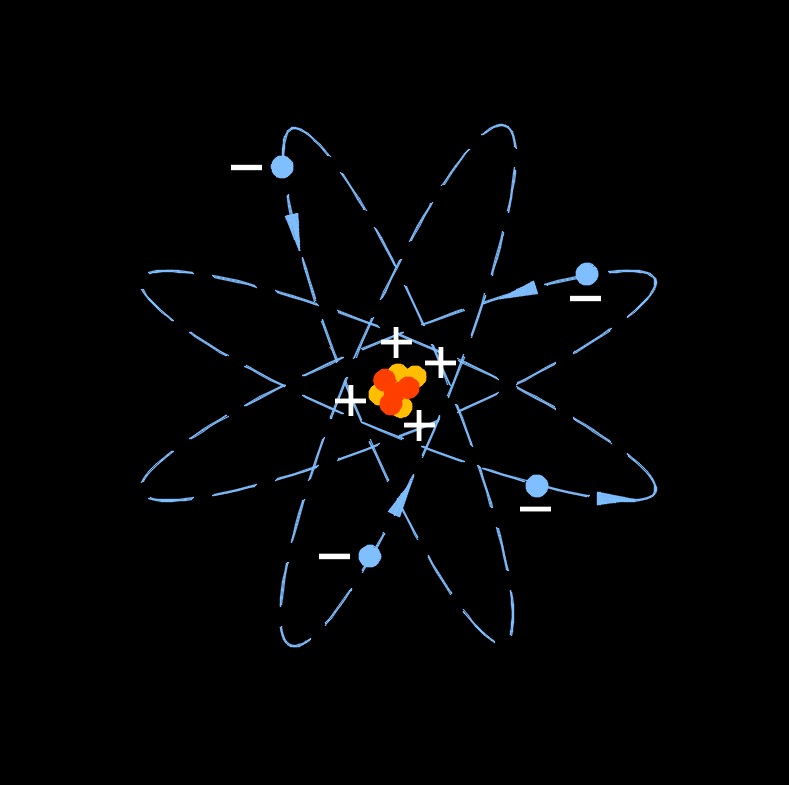Law of Conservation of Electric Charge
Law of conservation of electric charge states the sum of all the electric charges in any closed system remains constant over time. In other words, electric charge cannot be created or destroyed, it is conserved.
Electric charge is a fundamental property of matter, and it comes in two types: positive (+) and negative (-). Like charges repel each other, while opposite charges attract each other. This law ensures that the total amount of positive charge in a system is always equal to the total amount of negative charge. According to this law, in any physical process or interaction, the total amount of electric charge before and after the process remains the same. For example, in an electrostatic system, if two objects initially have a total charge of +5 units and -3 units, respectively, the total charge after bringing them into contact or separating them will still be +5 units and -3 units. The net charge of the system remains constant.
This law is of utmost importance in electromagnetism and the study of electric circuits. It provides a fundamental understanding of the behavior of electric charge, the principles of electrostatics, and the conservation of charge in various electrical and electronic devices.
Law of conservation of energy, also called conservation of energy, states that energy cannot be created or destroyed, but may be changed from one form to another.
Law of Conservation of Linear Momentum
Law of conservation of linear momentum states if the net external force acting on a system of bodies is zero, then the momentum of the system remains constant. According to this law the absence of external forces, the total momentum before an event or interaction is equal to the total momentum after the event or interaction. This means that the combined momentum of all objects within the system remains constant over time.
This law finds application in various areas of physics, such as collisions, explosions, and interactions between objects. It is particularly useful in analyzing and predicting the motion and outcomes of such events. It's important to note that this law applies to isolated systems, where no external forces are acting. In real world scenarios, it may be challenging to find completely isolated systems due to the presence of external influences such as friction or air resistance. However, the law is still valuable in providing insights and predictions in situations where external forces can be neglected or are negligible.
law of conservation of linear momentum formula |
||
|
\( \overrightarrow{p} = m \; \overrightarrow{v} \) (Law of Conservation of Linear Momentum) \( m = \overrightarrow{p} \;/\; \overrightarrow{v} \) \( \overrightarrow{v} = \overrightarrow{p} \;/\; m \) |
||
| Symbol | English | Metric |
| \( \overrightarrow{p} \) = linear momentum | \(lbm-ft\;/\;sec\) | \(kg-m\;/\;s\) |
| \( m \) = mass | \(lbm\) | \(kg\) |
| \( \overrightarrow{v} \) = linear velocity | \(ft\;/\;sec\) | \(m\;/\;s\) |
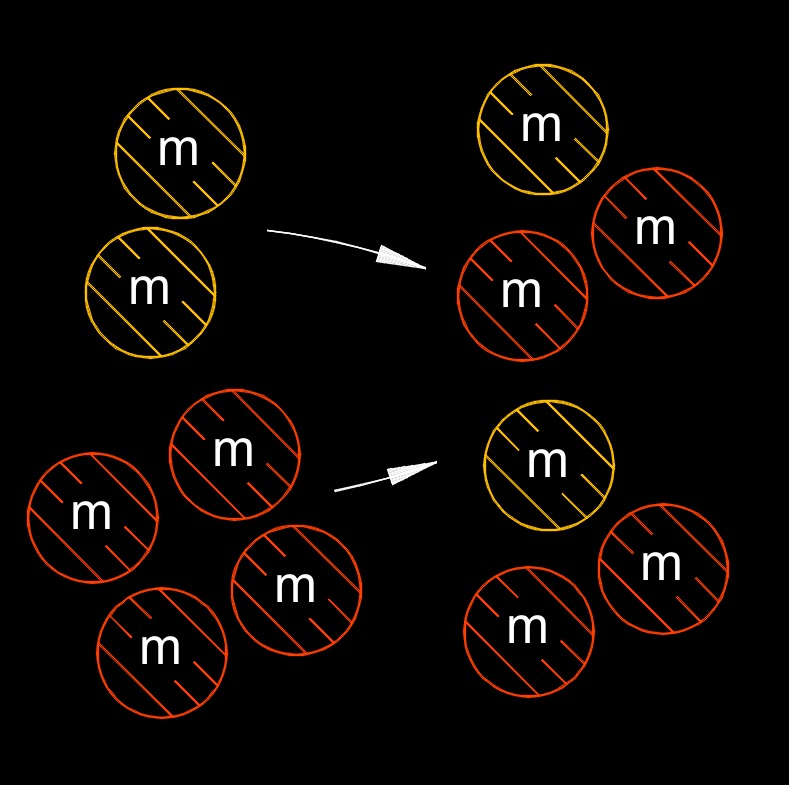Law of conservation of mass states in a closed system, the mass of the system cannot change over time. In other words, mass cannot be created or destroyed; it is conserved.
According to this law, in any physical or chemical process or interaction, the total mass of the reactants is equal to the total mass of the products. The atoms that make up the reactants rearrange themselves during the process, but the total number of atoms and their mass remains unchanged. This law is closely related to the principle of the conservation of atoms, which states that the number and types of atoms in a closed system also remain constant during a chemical reaction. This means that the total number of each type of atom in the reactants is equal to the total number of each type of atom in the products.
This law is a fundamental principle in stoichiometry, the branch of chemistry that deals with the quantitative relationships between reactants and products in chemical reactions. It forms the basis for balancing chemical equations and calculating the masses and quantities of substances involved in reactions. It's worth noting that in certain nuclear reactions or relativistic processes, where nuclear binding energies or energy mass equivalence is involved, there can be slight deviations from strict mass conservation. However, in everyday macroscopic chemical reactions, the law of conservation of mass is generally applicable and provides a fundamental understanding of mass transformations and interactions in closed systems.
law of conservation of mass formula |
||
| \( ( \partial \rho \;/\; \partial t ) + \triangledown \; \left( \rho \; v \right) = 0 \) | ||
| Symbol | English | Metric |
| \( \rho \) (Greek symbol rho) = density | \(lbm\;/\;ft^3\) | \(kg\;/\;m^3\) |
| \( t \) = time | \( sec \) | \( s \) |
| \( v \) = flow velocity field | \(ft\;/\;sec\) | \(m\;/\;s\) |
| \( \partial \) = divergence | - | - |
Law of Conservation of Mass-energy
The Law of conservation of mass-energy states that the total mass-energy of a closed system remains constant. It combines the principles of conservation of mass and conservation of energy into a unified concept. According to this law, the total amount of mass and energy in a closed system remains constant over time. Mass and energy can be converted from one form to another, but the total sum is conserved.
This principle arises from Albert Einstein's theory of relativity, specifically his famous equation E=mc², where E represents energy, m represents mass, and c represents the speed of light in a vacuum (a constant value). The equation shows that mass and energy are interchangeable and are two aspects of the same underlying physical entity. Mass can be converted into energy, and energy can be converted into mass. This is demonstrated in various phenomena, such as nuclear reactions, where a small amount of mass is converted into a significant amount of energy.
It's important to note that this law applies to closed systems where no mass or energy enters or leaves the system. In reality, energy and mass can be exchanged with the surroundings, and the law can be modified to account for these interactions. However, on a larger scale, the conservation of mass-energy remains a fundamental principle in understanding the behavior of the universe.
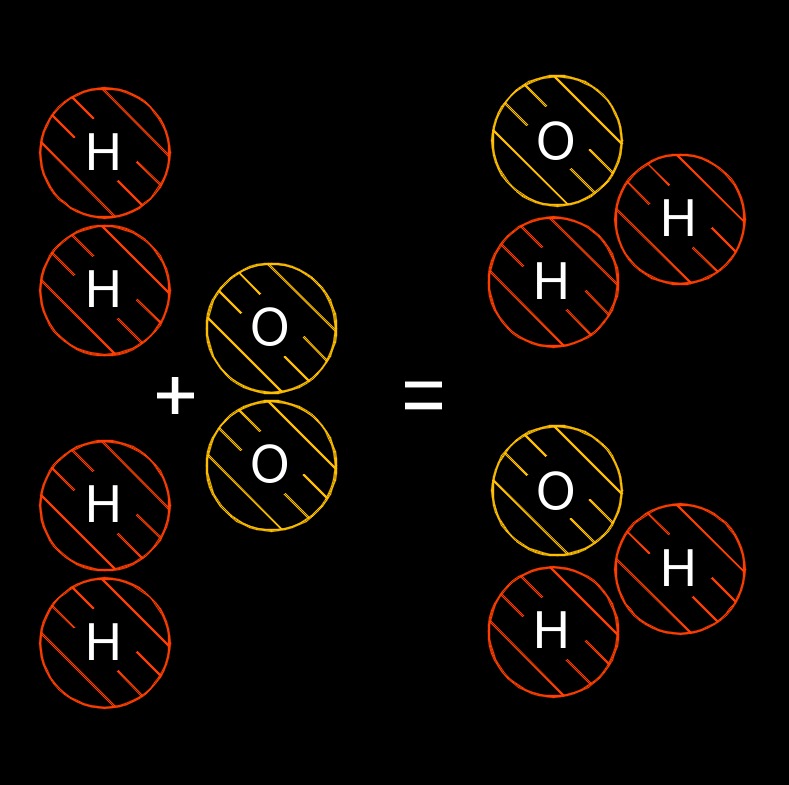Law of conservation of matter, also known as the Law of conservation of Mass, states that the mass of an object or collection of objects never changes over time, even when the matter changes form.
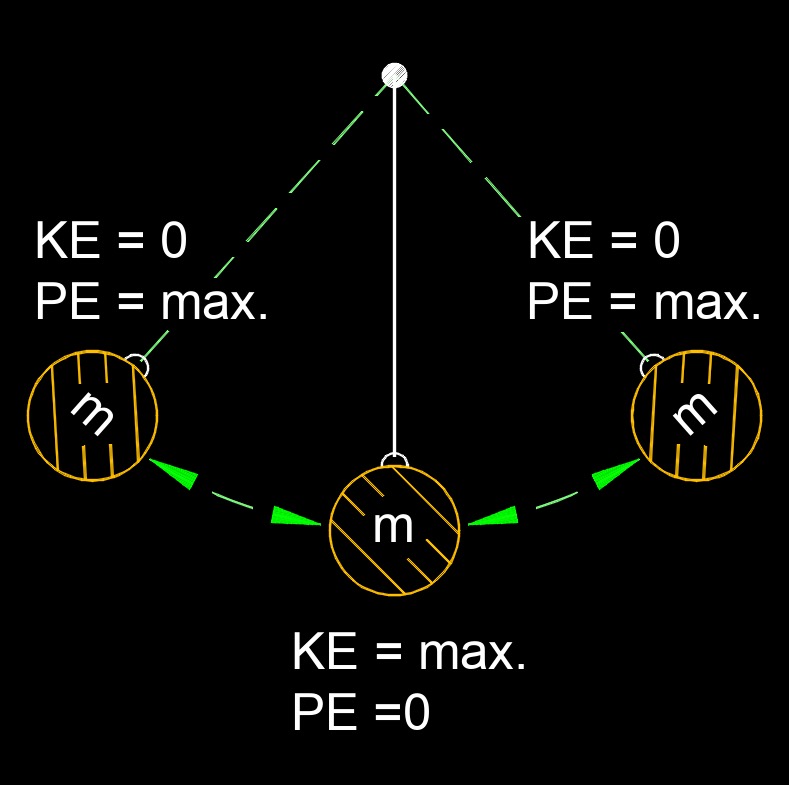
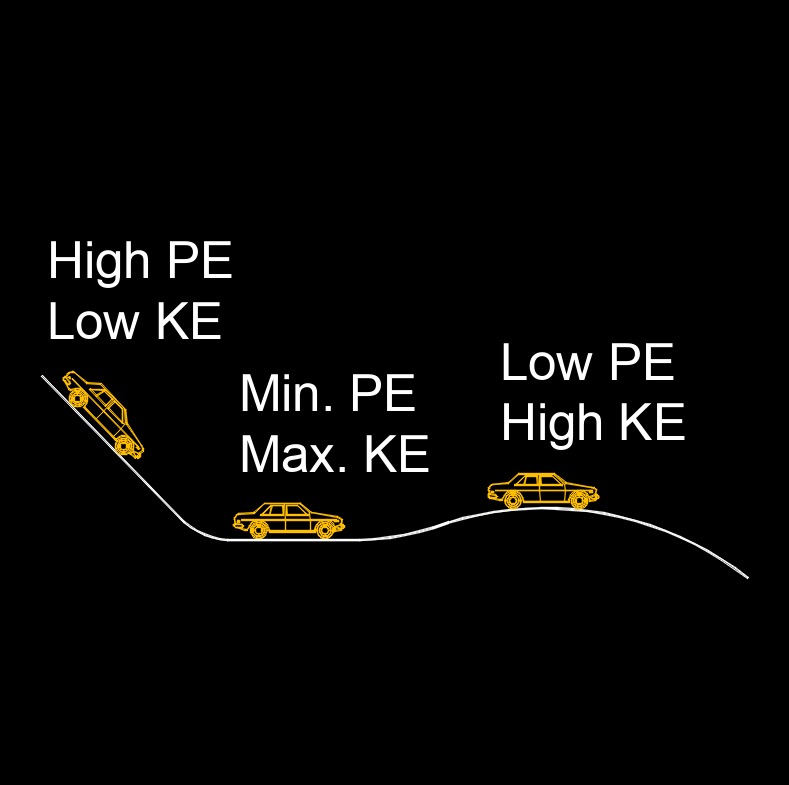Law of Conservation of Mechanical Energy
Law of conservation of mechanical energy states the total mecanical energy in a system remains constant as long as the only force acting are conservative forces. In other words, the sum of the kinetic energy and potential energy within the system remains constant over time.
According to this law, if a system is not influenced by external forces like friction or air resistance, the total mechanical energy (KE + PE) remains constant. This means that the energy may transfer between kinetic and potential forms within the system, but the total amount remains unchanged.
It's important to note that this law assumes an idealized scenario without energy losses due to factors like non-conservative forces or thermal energy dissipation. In real world situations, mechanical energy conservation is often an approximation, and energy may be lost or transformed into other forms.
law of conservation of mechanical energy formula |
||
|
\( PE_i + KE_i = PE_f + KE_f \) (Law of Conservation of Mechanical Energy) \( PE_i = PE_f + KE_f - KE_i \) \( KE_i = PE_f + KE_f - PE_i \) \( PE_f = PE_i + KE_i - KE_f \) \( KE_f = PE_i + KE_i - PE_f \) |
||
| Symbol | English | Metric |
| \( PE_i \) = initial potential energy | \( lbf-ft \) | \(kg-m^2\;/\;s^2\) |
| \( KE_i \) = initial kinetic energy | \( lbf-ft \) | \(kg-m^2\;/\;s^2\) |
| \( PE_f \) = final potential energy | \( lbf-ft \) | \(kg-m^2\;/\;s^2\) |
| \( KE_f \) = final kinetic energy | \( lbf-ft \) | \(kg-m^2\;/\;s^2\) |
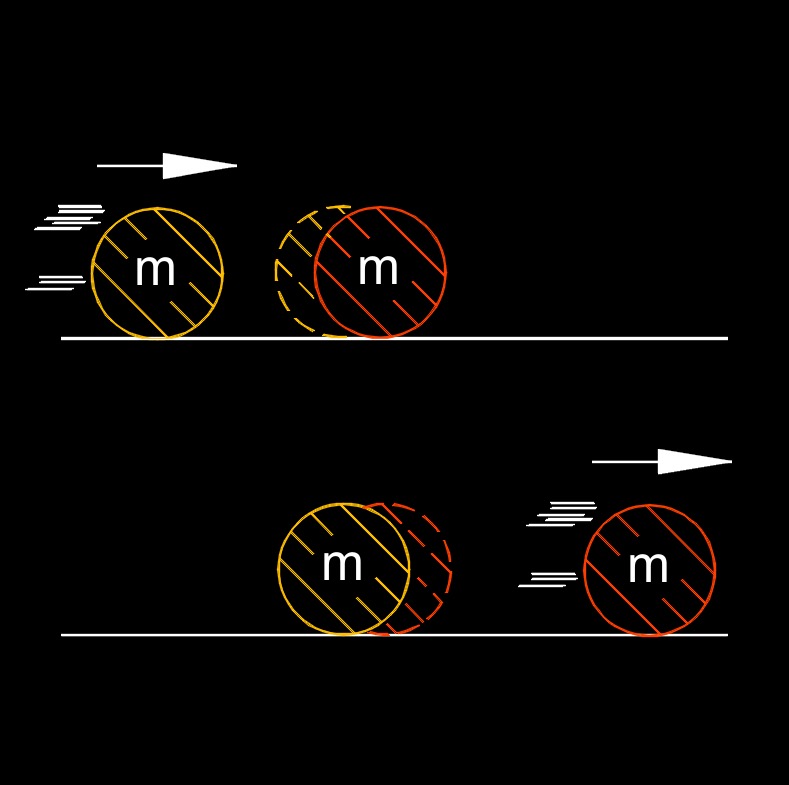
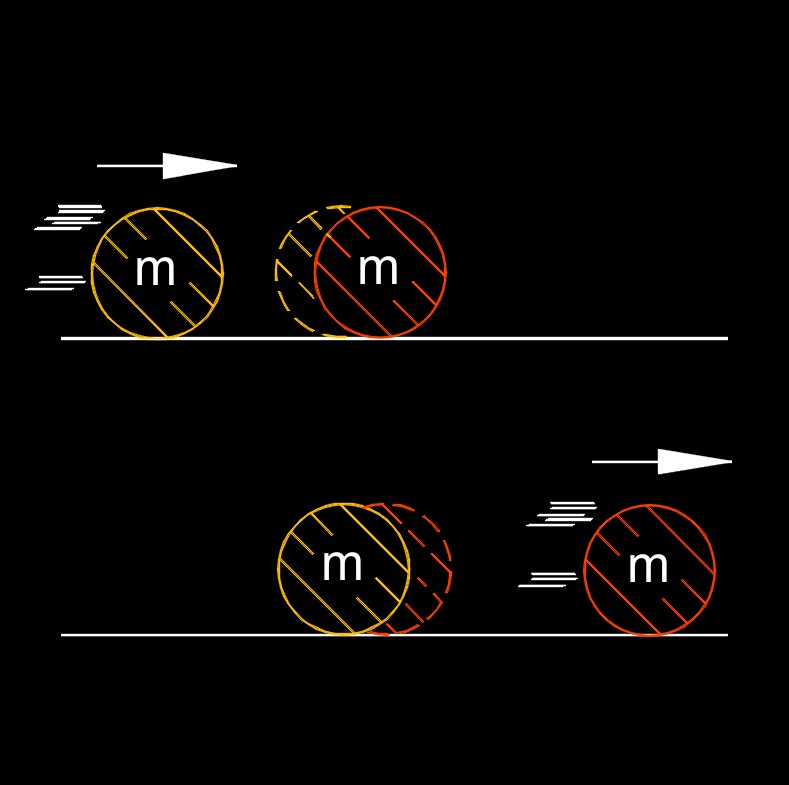Law of Conservation of Momentum
Law of conservation of momentum states that the total momentum of an isolated system remains constant if no external forces act upon it. In other words, the total momentum before an event or interaction is equal to the total momentum after the event or interaction. Momentum is a vector quantity that depends on an object's mass and velocity.
According to the law of conservation of momentum, if no external forces (such as friction or collisions with other objects) are acting on a system, the total momentum of that system will be conserved. This law finds broad applications in various areas of physics, such as mechanics, collisions, fluid dynamics, and particle physics. It helps in analyzing and predicting the motion and interactions of objects and particles in different physical scenarios.
Law of conservation of momentum formulas |
||
|
\( p_i = p_f \) \( p_i + p_f = p_i^{\prime} + p_f^{\prime} \) \( m_i \; V_i + m_f \; V_f = m_i \; V_i^{\prime} + m_f \; V_f^{\prime} \) |
||
| Symbol | English | Metric |
| \( p_i \) = the initial system's momentum | \(lbm-ft\;/\;sec\) | \(kg-m\;/\;s\) |
| \( p_f \) = the final system's momentum | \(lbm-ft\;/\;sec\) | \(kg-m\;/\;s\) |
| \( m_i \) = initial mass | \(lbm\) | \(kg\) |
| \( V_i \) = initial volume | \(ft^3\) | \(m^3\) |
| \( m_f \) = final mass | \(lbm\) | \(kg\) |
| \( V_f \) = final volume | \(ft^3\) | \(m^3\) |
